連立方程式の解法
数値計算で連立方程式を解く方法として、ガウス・ジョルダン法(Gauss Jordan Method)があります。
ガウス・ジョルダン法は、連立方程式から係数行列を作り、その係数行列を単位行列になるように掃き出しを繰り返す手法です。
ここでは、ガウス・ジョルダン法の考え方とアルゴリズム、例題として3元連立方程式に適用した場合のC言語プログラムを記述します。
ガウス・ジョルダン法の考え方
3元連立方程式を考えます。

①、②、③のように3元連立方程式が与えられたとき
まず、①式をa_11で割ってx_1の係数を1とした式①’を作ります。
次に、②式から先ほど作成した①’式にa_21をかけたものを引きます。
これを②’式とします。
さらに、③式から①’式にa_31をかけたものを引いた式を③’式として作ります。
ここまでをまとめると次のような式に変形できます。

個の式変形によって②式、③式からx_1の項がなくなりました。
同じような考え方で、①’式、③’式からx_2の項をなくします。

まず、②’式をa_22で割って、②”式を作ります。
この②”式をもとに、①’式、③’式からx_2の項がなくなるように②”式に係数をかけて引くと①”式、③’’式が得られます。
同じようにして、③”式をもとに①’’式、②”式からx_3の項をなくします。式変形すると次のように①”’、②”’、③”’が得られます。

この式で得られたb1”’、b2”’、b3”’がそれぞれx_1、x_2、x_3の解となります。
プログラムにするには
ガウス・ジョルダン法の考え方をプログラムに落とし込むにはどうするかというところをまとめます。
これをプログラムで記述するには、次のような係数行列を作ります。

3元連立方程式の場合は、3行4列の係数行列となります。
この係数行列に対して掃き出し演算をすることで、係数行列が単位行列になるように計算を繰り返します。

赤色の丸枠で囲ったa_11、a_22、a_33をピボットと呼びます。
ピボットを1にして、ピボット以外のa_ijを0になるように計算したときの4列目の値β1、β2、β3が解となります。
これを手順化してプログラムに落とし込んでいきます。
アルゴリズム
①ピボットを1行1列からn行n列に移動しながら次の処理を繰り返します
②ピボットの行kの要素(a_kk, a_(kk+1),…, a_kn, b_k)をピボット係数(a_kk)で割ります
③ピボット行以外の各行について次の処理を繰り返します
(各行)ー(ピボット行)×(係数)
この①から③により連立方程式を解くアルゴリズムがガウス・ジョルダン法になります。
具体的に3元連立方程式の例題を解いてみたいと思います。
例題
次の3元連立方程式をガウス・ジョルダン法で解いてみます。
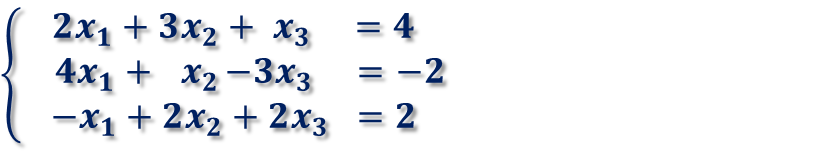
まず、係数行列を作ります。
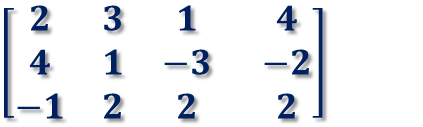
次に、1行1列をピボットにして、掃き出し操作をします。

1行1列の係数が2なので1行目を2で割ります。
2で割った1行目を使って2行1列、3行1列の1列目を0にします。

2行目は、1行目の要素に4をかけたものを引くことで0になります。
同じように3行目は、1行目の要素にー1をかけたものをひくことで0になります。
これで、1行1列をピボットにした操作は終了です。
ここで、ピボットを2行2列に移します。
操作は、1行1列のピボットのものと同じです。

2行2列のピボット係数ー5で2行目を割ります。
そして、1行2列目、3行2列目の2列目を0にします。

同様にして、3行3列をピボットにした場合です。

3行3列のピボット係数ー1で3行目を割ります。
1行3列、2行3列の3列目を0にします。

これで、操作はすべて終了です。
係数行列は、ピボット係数が1となり、それ以外は0となっています。
このときの4列目が求める解となります。

この結果をもとにして、実際にプログラムに実装し、同じ結果が得られるか確認してみたいと思います。
例題のプログラム実装
先ほどの例題のサンプルプログラムになります。
係数行列をaという2次元配列で定義しています。
変数pにピボット係数を格納し、係数行列aを更新しています。
掃き出し操作がすべて完了した時点で、結果を出力しています。
解は、係数行列の4列目に格納されているのでa[k][N](k=0,1,2)を出力としています。
c:\prog\algorithm>gauss_jordan
x1 = 2.000000
x2 = -1.000000
x3 = 3.000000
test end実装したプログラムを実行した結果です。
手計算の結果と同様にx_1=2、x_2=-1、x_3=3が得られています。

コメント