K-means法

K-means法とは

K-means法（K平均法）は、クラスタリング手法のひとつです。

クラスタリングとは、画像や音声などのパターン認識を行うときに特徴の近いものをまとめてグループ化する処理のことです。

グループ化したそれぞれのパターンをクラスタと呼びます。

クラスタリングの手法として、NN法（Nearest Neighbor method）やK平均法(K-means method)があります。

ここでは、K-means法のアルゴリズムとサンプルプログラムを書いていきます。

サンプルプログラムは、すべての動作を保証したものではないので、使用する場合は、十分ご確認の上、使用される方の責任のもとお使いいただくようお願いします。

K-means法のアルゴリズム

K平均法は、分類したいデータ列に対してK個のクラスタを用意して、各データがK個のクラスタのうちどのクラスタに最も近いかユークリッド距離を求めることにより決定します。

最も近い距離にあるクラスタをそのデータの分類とします。

この分類を全データに対して行った後、クラスタの更新を行います。

クラスタの更新は、クラスタに属するすべてのデータの平均値より求めた値により行います。

クラスタの更新処理で元のクラスタ値と変わらなければ、処理を終了します。

値が修正されていれば、データ列の分類を更新したクラスタに対して行い、処理を繰り返します。

K平均法のアルゴリズムをまとめます。

K平均法のサンプルプログラム

K平均法のプログラム例を以下に示します。

この例では、二次元空間を４つの領域に区分して、８個の二次元データがどの区分に属するかを出力するようにしています。

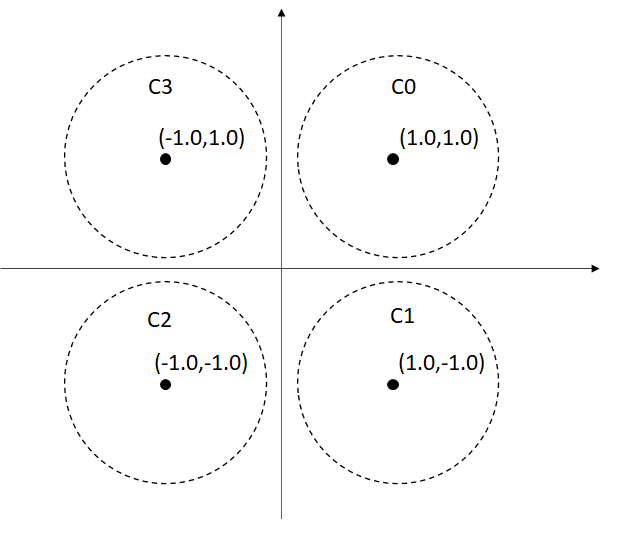
クラスタは、初期値として上図のような４点を与えています。

double dInitCenterPosit[D_MAX_CLASS_SIZE][D_DIMENSION] =
{
    {1.0,1.0},
    {1.0,-1.0},
    {-1.0,-1.0},
    {-1.0,1.0}
};

それに対して、テストデータとして

double dPattern[D_MAX_PATT_SIZE][D_DIMENSION] =
{
    {-10.0,3.0},
    {10.0,8.0},
    {-1.0,-2.0},
    {1.0,-3.0},
    {5.0,3.0},
    {-2.0,-8.0},
    {-3.0,6.0},
    {7.0,-4.0}
};

というような８個のデータを用意しました。このデータを分類します。

fdDistance()は、クラスタとデータの距離を計算する関数で、fiClassDetermination()は、クラスタとデータの距離で最小となるクラスタの番号を取得するための関数となっています。

サンプルプログラムの実行結果は、以下のようになりました。

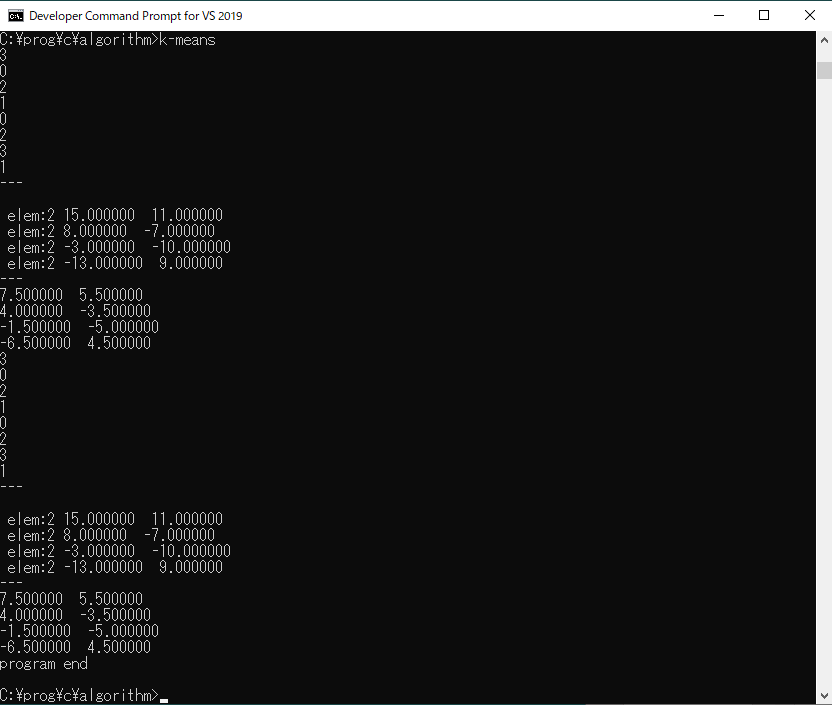
初期クラスタに対して、１回目の処理で次のような結果になっています。

これに対して２回目の処理結果も同様となり、クラスタの更新が行われなかったので、処理が終了しています。各クラスタには、それぞれ２個のデータが分類されているのがわかります。

また、この分類処理によりクラスタは次のように更新されています。

7.500000  5.500000
4.000000  -3.500000
-1.500000  -5.000000
-6.500000  4.500000

まとめ

ここまで、パターン認識のクラスタリング手法としてK平均法をみてきました。

二次元空間での分類を例として実際にプログラムを実行してみて確認しました。

実際のパターン分類を行うには、特徴量を特徴空間にマッピングして行う必要があります。

今後、ここでのサンプルプログラムをもとに実際の画像などを使って分類処理を行っていきたいと思います。