ニュートン法とは
ニュートン法は、非線形方程式の解を求める手法で、逐次近似法のひとつです。
非線形方程式の解を求める手法として、直接探索法である二分法があります。二分法については、こちらにまとめています。

ニュートン法は、二分法と違い、あらかじめ解の存在範囲を知る必要がなく、二分法よりも早く解に収束する特徴があります。
ニュートン法の欠点としては、初期値の与え方によっては、収束しない場合もあり、常に解が求められる保証はないという点があげられます。
ここでは、ニュートン法の考え方、アルゴリズムとサンプルプログラムを記載します。
ニュートン法による非線形方程式の解法
ニュートン法は、非線形方程式のある点での接線とX軸との交点を求め、その交点における接線からさらにX軸との交点を求めていくという手順を反復することで、近似解を求める手法です。
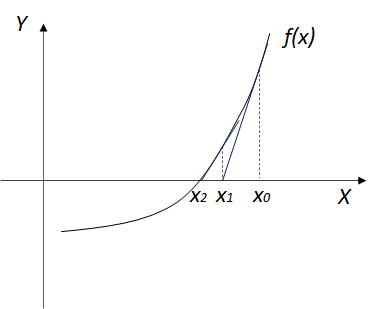
上の図において、まず、非線形方程式f(x)に対して初期値x0における接線を求めます。
次に、その接線とX軸との交点を近似解x1とします。
x1から収束判定値を求めて、その値が基準内となるまでこの手順を繰り返していきます。
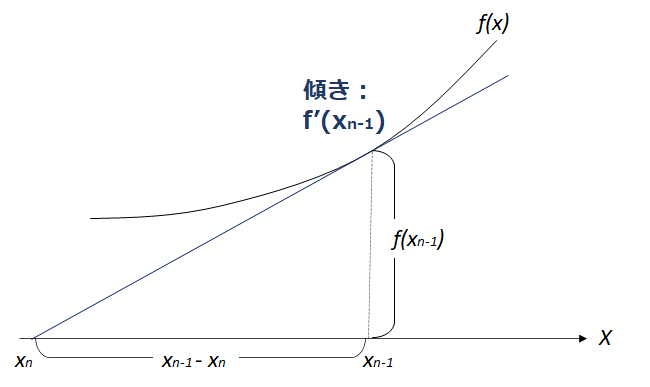
接線の傾きをf’(xn-1)は
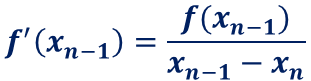
で求まるので、次の近似解は、
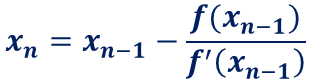
で求まります。
この計算式を繰り返すことで近似解が得られるということになります。
ニュートン法のアルゴリズム
ニュートン法のアルゴリズムをまとめます。
ニュートン法は、次の手順によって非線形方程式の解を求めます。
ここで、収束判定は、次の式で行います。
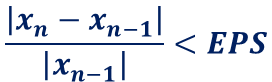
ニュートン法のサンプルプログラム
このサンプルプログラムでは、
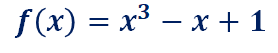
という非線形方程式に対しての近似解を求めています。
プログラムでは、あらかじめ、f'(x)を
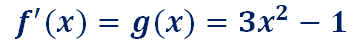
として、定義しています。
判定基準はEPSで与えていて、最大50回の反復計算で収束しない場合は、終了となります。
ニュートン法による連立非線形方程式の解法
ここまでは、1変数の非線形方程式に対して、ニュートン法を用いて数値解を得る方法についてみてきました。
次に、複数の非線形方程式からなる問題に対して、ニュートン法を適用していきたいと思います。
連立非線形方程式の場合、考え方は1変数の場合と同じで、変数がベクトル化していきます。それに伴って、傾きを求める部分では、ヤコビアン(ヤコビ行列)を使います。
初期値はベクトル

となります。
xの更新もベクトル化されて
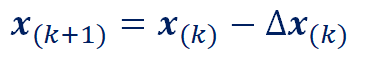
となり、Δx(k)は、
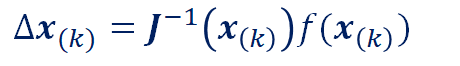
で表されます。ここで、J をヤコビアン(ヤコビ行列)といいます。
ヤコビアンは、xベクトルの各要素を偏微分した行列
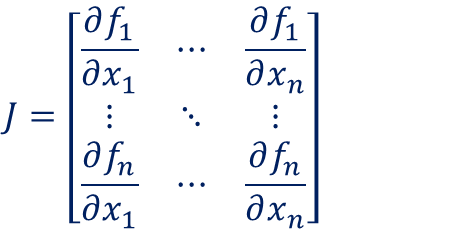
です。
数値計算では、ヤコビアンの逆行列は、求めにくいので
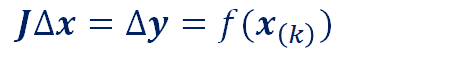
よりΔx を求めることになります。
収束判定の条件は、ベクトルΔy の絶対値が最大のものを用いて
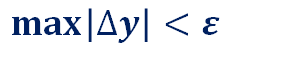
とします。
連立非線形方程式の例題
次の連立非線形方程式をニュートン法で解いてみたいと思います。
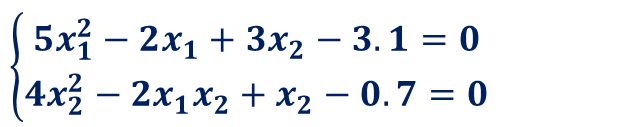
この例でのヤコビアンは、次のようになります。
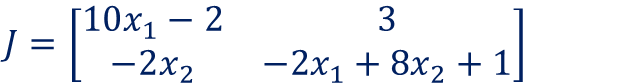
サンプルプログラムを作成しました。
実行結果は、次のようになります。
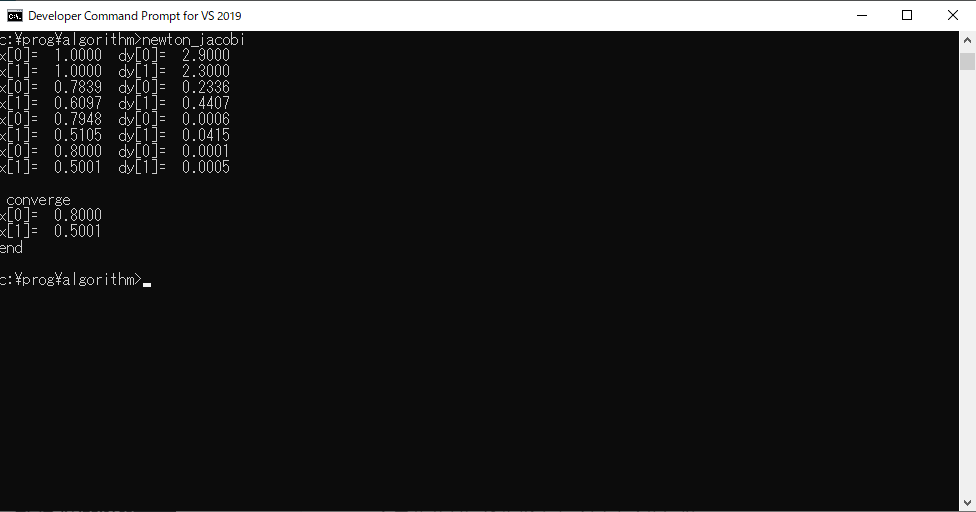
初期値、(x0,x1)=(1.0,1.0)から始まり、3回目でdyの絶対値の大きい方の値が、収束判定基準の0.001より小さくなっているので、ここで収束条件を満たし、解を出力しています。解は、(x0,x1)=(0.8,0.5001)となります。



コメント
ニュートン法による連立非線形方程式の解法のプログラムにおいて初期近似値に√を使用したいのですが、「定数式では関数呼び出しを使用できません」というメッセージが表示されます。どうすればよいでしょうか。
ご質問ありがとうございます。変数の初期化は、定数式である必要があるため、その中に関数を入れ込めません。
ですので、ルート計算した値を初期値に代入するか、main関数内でsqrt関数を使って値を代入するかかと思います。
x_init[0] = sqrt(2.0);
x_init[1] = sqrt(3.0);
のように記述すれば、エラーは回避できるかと思います。
ありがとうございます!