4次のルンゲ・クッタ法とは
ルンゲ・クッタ法(Runge-Kutta method)は、微分方程式の解を求める手法で、べき級数を4次の項まで近似するため、4次のルンゲクッタ法と呼ばれています。
微分方程式は、解析的に解くことが難しい場合もあり、そのようなときに数値計算による解法は非常に有効です。
ここでは、4次のルンゲ・クッタ法のアルゴリズムについてとC言語によるサンプルプログラムを書いていきます。
4次のルンゲ・クッタ法のアルゴリズム
1階の微分方程式
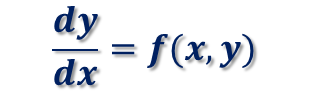
に対して、一つの解y=y(x)をもつものとします。
初期値x_0に対するyの値y_0が既知であるとき
x_0から一定の刻み幅hを加算した点をx_1とすると
x_1に対するyの値y_1をy_0、及び、x_0から求めます。
これをy_2、y_3、y_4、…、y_nというように逐次計算していきます。
4次のルンゲ・クッタ法では、x_nのときのyの値y_nが既知の場合、
x_n+1におけるy_n+1の値は、次の式で求めることができます。
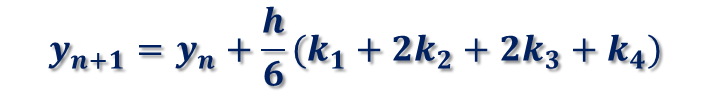
ここで、k_1、k_2、k_3、k_4は、次式で与えられます。
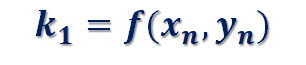
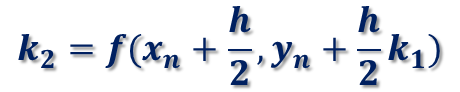
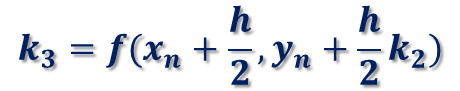
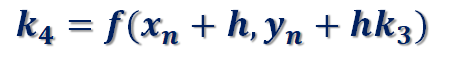
k_1は、(x_n,y_n) を通る解曲線の接線の傾き、k2_は、(x_n+h/2,y_n+h/2 k_1) を通る解曲線の傾き、k_3は、(x_n+h/2,y_n+h/2 k_2) を通る解曲線の接線の傾き、k_4は、(x_n+h,y_n+hk_3) を通る解曲線の接線の傾きを表します。
ルンゲクッタ法では、このk_1,k_2,k_3,k_4という接線の傾きを表す係数に重みづけをして平均化した値を使って近似解を更新していきます。
4次のルンゲ・クッタ法の誤差は、刻み幅hの5乗オーダーとなります。

アルゴリズムは、次のようになります。
4次のルンゲ・クッタ法のサンプルプログラム
次の2階の微分方程式を4次のルンゲ・クッタ法を使って解いてみます。
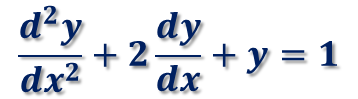
ただし、初期値を

とします。
2階微分方程式のままでは、ルンゲ・クッタ法が適用できないので、この方程式を1階の2元連立微分方程式に分解します。

とおくと、与えられた2階微分方程式は、
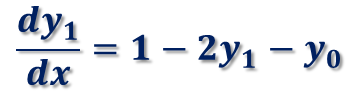
と書けます。この二つの微分方程式を解いていきます。
プログラム例を以下に示します。
このサンプルプログラムでは、刻み幅を0.5として、x=0からx=10までの解を求めています。このプログラムの実行結果は、次のようになりました。
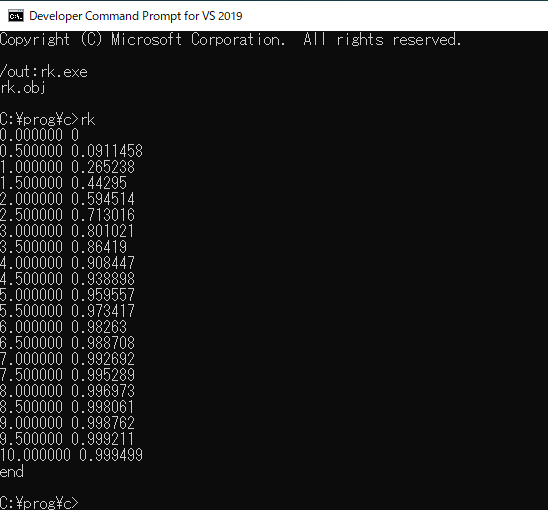

まとめ
ここまで、微分方程式の数値計算として4次のルンゲ・クッタ法をみてきました。
高階の微分方程式に対しても、1階の連立微分方程式に分解することで、ルンゲ・クッタ法を適用できるということを例題から確認できました。
様々な物理現象や工学的問題は、微分方程式で記述されます。そのような問題に対して解を計算する手法としてルンゲ・クッタ法は、有用ではないかと思います。


コメント