二分法とは
数値計算による非線形方程式の解法として、二分法というアルゴリズムがあります。
二分法は、データ範囲を半分に分け、解が半分に分けたどちら側にあるかを調べるということを繰り返す手法です。この繰り返しにより、調べる範囲を狭めていき、最終的に方程式の解を近似します。
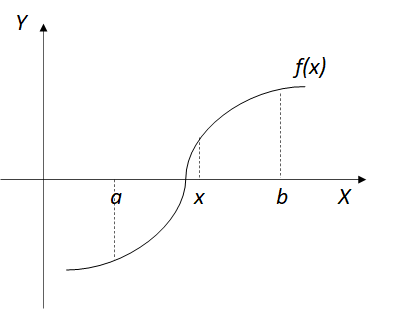
上の図は、二分法のイメージ図です。
解を求めようとしている関数f(X)に対して、f(a)<0でf(b)>0となるX軸上の点a,bを設定します。
ただし、点a,bは、その区間[a,b]の内でf(X)が1回だけX軸と交わるという条件を付けます。つまり、区間[a,b]でf(X)は、1つだけ解をもつということがわかっている前提となります。
この区間[a,b]の中点xを求めて、そのxに対してf(x)の値が正か負かを判定することで、解が区間[a,x]側にあるか、区間[x,b]側にあるかがわかります。これにより、解のある範囲が半分に絞れます。この半分の範囲に対して同じように解の所在を探索していくことで、数値解を求めます。
このように解の探索範囲を半分に分割することを繰り返すというところからこの手法は、二分法と呼ばれています。
二分法アルゴリズム
二分法のアルゴリズムは次のようになります。
中点は、
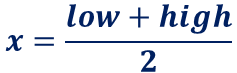
で求まります。
また、収束判定基準(ESP)は、適切な制度の値に設定し
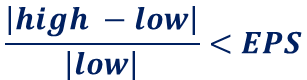
を満たすとき、収束したと判断し、その時のxを解とします。
二分法プログラム
二分法のサンプルプログラムです。
このプログラムでは、収束判定基準値を
1.0E-8(Eは、10のべき乗)に設定していて、最大50回の繰り返しで収束しない場合は、処理を終了させます。



コメント