数値積分
微分は、ある瞬間の変化を捉えることであるのに対して、積分は、経過時間における蓄積量を捉えることであるといえます。
言い方を変えると、微分は、接線の傾きを求めることで、積分は、面積を求めることです。
数値積分とは、計算機上で積分計算を行うというもので、近似的に解を求めるため、理論的な積分計算との間に誤差が生じます。数値積分では、この誤差を許容範囲に収める必要が出てきます。
それでは、実際に、半径2[m]の1/4円の面積を求める例を使って台形面積近似による数値積分のプログラムを作ってみたいと思います。

求める面積は、上図の青色で塗られた部分になります。
理論計算上は、円の面積は、πr2 で求まるので
1/4円の面積は、3.141592[m2]です。
これを、数値積分で求めてみます。
台形面積近似による方法
ここでは、台形の面積を加算する手法で数値積分を行います。
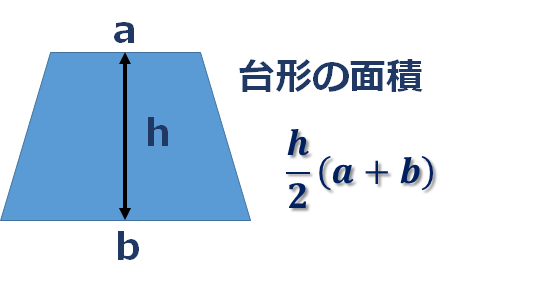
台形の面積は、次の式で求まります。
この台形の面積を足し合わせていくことで、求めたい1/4円の面積を近似していきます。
求める1/4円を、台形に分割してみます。
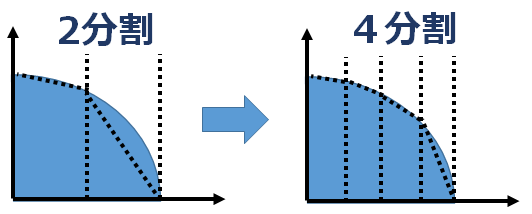
まず、2分割の場合を考えてみます。2分割の場合は、1つの台形と1つの直角三角形に分割できます。
直角三角形の面積は、底辺×高さ÷2で求まります。
これは、台形の面積の公式でa=0としたときと同じです。
なので、直角三角形の面積もa=0の台形の面積とみなすことができます。
つまり、1/4円を2分割したときは、2つの台形の面積を求めることで近似できるとなります。
図から見てもわかりますが、この近似だとかなり粗いものになります。
次に、4分割の場合を考えてみます。この場合、4つの台形に分割できるので、それぞれの台形の面積を求めることで、1/4円の面積を近似します。2分割に比べると、円周部分の誤差が小さくなっているのが見てとれます。
このように、分割数をさらに細かくすることで、誤差を小さくして、1/4円の面積を近似するというのが、台形面積近似による数値積分の手法になります。
台形面積近似手法の計算式
前述の考え方を一般化していきます。
半径2[m]の1/4円ということで、0から2まで領域をm個に分割すると、その一つ一つの幅hは、h = 2 / m となります。

ある点aから次の点(a+h)の区間の台形の面積は、
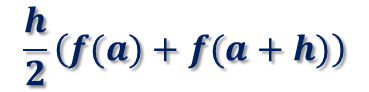
です。
次の領域(a+h)から(a+2h)の台形の面積は、
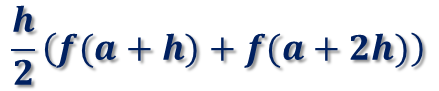
になります。
m個のすべての台形の面積を足し合わせると
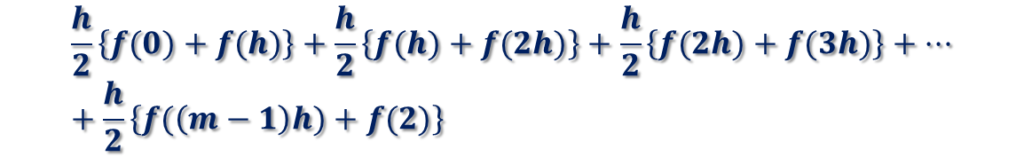
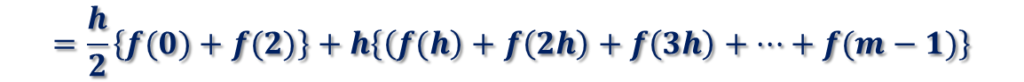
となります。これが、求める面積の近似値です。
サンプルプログラム
サンプルプログラムです。区間を50分割しています。
f(0)=2とf(2)=0なので、sumの初期値として、h/2{f(0)+f(2)}=hを代入して
h{f(h)+f(2h)+……+f(m-1)}をfor文の繰り返し処理で計算しています。
結果は、次のようになりました。
分割数50の場合、
c:\prog\algorithm>integ
3.138269分割数を100にした場合、
c:\prog\algorithm>integ
3.140417分割数を1000にした場合、
c:\prog\algorithm>integ
3.141555分割数を10000にした場合、
c:\prog\algorithm>integ
3.141591という結果になります。
理論値は、3.141592なので、分割数を増やすと誤差が小さくなるのがわかります。
分割数を増やすと、計算量も増大するので、要求される計算精度に応じた分割数を設定する必要があります。



コメント